LASSO, Robert Tibshirani, 1996

写在前面的话：这学期修了《广义线性模型》这门课，期中考的时候钟威老师要求我们阅读变量选择领域的几大经典文献，并各写一篇summary。本文即是我期中作业的一部分，介绍统计大神Tibshirani的神作–《Regression Shrinkage and Selection via the Lasso》.

Motivation and Method

当我们面对的数据集中包含非常多的解释变量时，传统的OLS估计量往往无法满足数据分析的需求。此时我们希望从变量集中挑选出部分变量，降低模型复杂性，提高模型的解释能力。由于传统的两个变量选择方法，子集选择法和岭回归法都有相应的不足之处。其中子集选择法虽然提供了精炼的模型，但该方法非常不稳定，数据集的细微改变就会带来基本不一样的模型；而岭回归法的结果虽然具有稳定性，但它却无法将变量的系数压缩到0，即无法提供模型的解释能力。

在这个背景下，Robert Tibshirani于1996年提出了著名的LASSO(Least Absolute Shrinkage and Selection Operator),其动机来源于Breiman(1995)提出的一个想法——Non-negative garotte(NNG), 即假定我们有数据\((X^{i},y_{i}), i = 1,2,…,N \),其中\(X^{i}=(x_{i1},…,x_{ip})^{T}\)和\(y_{i}\)分别为解释变量和被解释变量的观测值。在一般的回归模型中，我们假定观测值相互独立或者是被解释变量\(y_{i}\)在给定解释变量\(x_{ij}\)的条件下相互独立。需要注意的是，这里的\(x_{ij}\)是标准化后的数据，即\(\frac{1}{n}\sum_{i}x_{ij}=0\),\(\frac{1}{n}\sum_{i}x_{ij}^{2}=1\)。
令

$$\hat{\beta}=(\hat{\beta}_{1},...,\hat{\beta}_{p})^{T}$$

此时NNG可以表示为:

$$\sum_{i=1}^{N}(y_{i}-\alpha-\sum_{j}c_{j}\hat{\beta}_{j}^{0}x_{ij})^{2} \qquad s.t. \qquad c_{j}\geq0,\sum_{j}c_{j}\leq t$$

NNG的原理是再最小二乘估计的基础上，通过加入一些非负因子的惩罚将回归系数压缩，并且这些非负因子惩罚的总和由一个常数$t$来控制。

虽然对于子集选择法来说，NNG的误差较小，并且可以删除真实模型中很多接近0但是非0的系数，但是NNG也存在一定的缺点，比如该方法过度依赖于最小二乘估计，在最小二乘估计不能得到很好结果的情况下，NNG的估计结果也存在较大偏差。而 Tibshirani提出的LASSO可以避免最小二乘估计带来的这两类问题。

LASSO的估计量\((\hat{\alpha},\hat{\beta})\)为：

$$(\hat{\alpha},\hat{\beta})=arg\min\{\sum_{i}^{n}(y_{i}-\alpha-\sum_{j=1}^{p}\beta_{j}x_{ij})^{2}\} \qquad s.t. \qquad \sum_{j=1}^{p}|\beta_{j}| \leq t$$

其中，\(t \geq 0\)是调和参数，此时对任意t，\(\hat{\alpha}=\bar{y}\)。不失一般性，我们可以假定\(\bar{y} = 0\)从而省略掉\(\alpha\)，根据拉格朗日乘子(Lagrange Multipliers)方法可得：

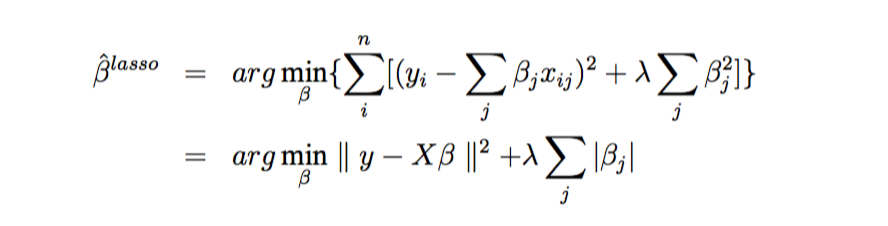
从这里我们可以看出，LASSO与子集选择法的不同之处在于：子集选择法的选择过程是一个离散且无序的过程，一些变量保留下来，而另一些则被提出模型。而由于\(L_{1}\)惩罚的自然属性，LASSO构造的模型是稀疏的，并且能够同时实现连续的变量收缩和自动地选择变量。

对于LASSO和岭回归，我们可以从图1中看到一个直观的对比：

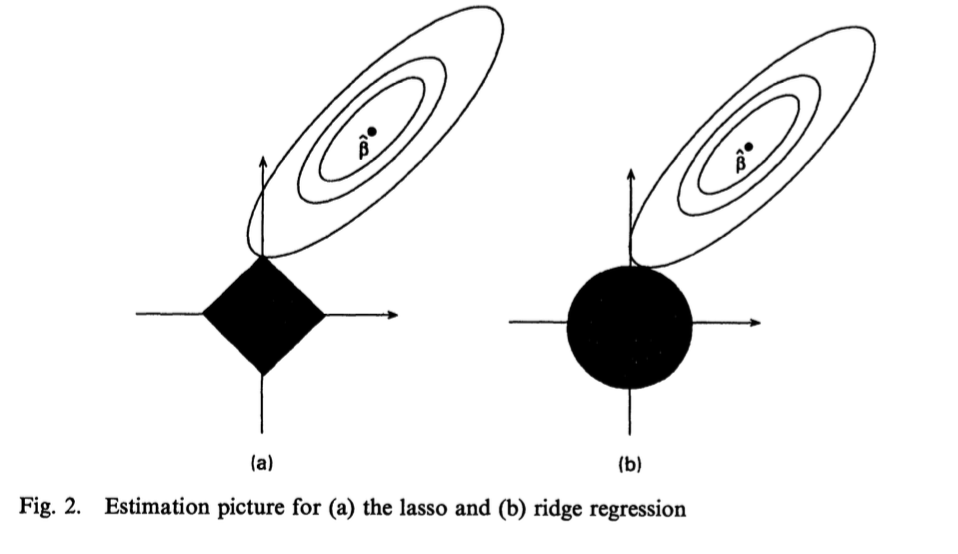
图1给出了误差和约束函数的曲线。在只考虑两个参数的情况下，图中阴影部分分别是LASSO约束

$$|\beta_{1}|+|\beta_{2}| \leq t$$

和岭回归约束

$$\beta_{1}^{2} + \beta_{2}^{2} \leq t^{2}$$

区域，而椭圆则是残差平方和的曲线。两种方法都是在椭圆曲线与约束区域相交时获得解，由于LASSO的约束区域是菱形，如果解在某个角上，则另一个参数等于零。相反，岭回归方法则无法将系数压缩到0。

图2中分别展示了子集选择法、岭回归法、LASSO和NNG的参数估计量的函数形状：

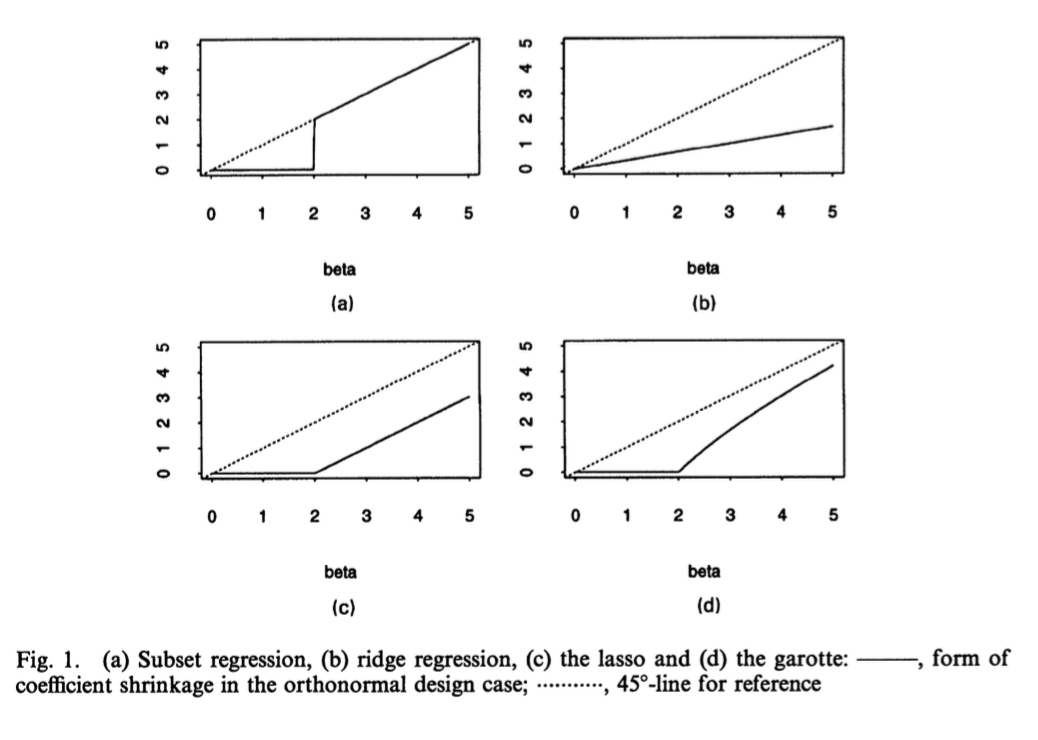
从图2中我们可以看出：岭回归法对最小二乘估计值做等比例规模变化，而LASSO是将系数较小的估计值压缩到0，对于系数较大的估计值则是减去一个常数。同时我们还发现NNG和LASSO十分类似，对于系数较大的估计值，NNG的压缩力度较小。

Contribution and Application

使用LASSO方法进行变量选择的关键在于调整参数$\lambda$的选取。Tibshirani(1996)介绍了三种选择$\lambda$的方法：交叉验证法、广义交叉验证(GCV)和风险无偏估计法。严格来说，前两种方法适用于解释变量随机的情况，而第三种方法则用于解释变量非随机的情况。但是由于在实际应用中无法完全区分这两种场景，所以我们通常选择最便捷的方法。

广义交叉验证(Generalized Cross-Validation)：

$$GCV(\lambda)=\frac{rss(\lambda)}{N(1-\frac{p(t)}{N})^{2}}$$

其中\(rss(\lambda)\)是残差平方和，\(p(t)=tr{X(X^{T}X+\lambda W^{-})^{-1}X^{T}}\)

由于LASSO的目标函数在\(\beta_{j}=0\)处是不可微的，因此简单的优化算法比如Newton-Raphson并不能直接使用。Tibshirani还提出了使用具有连续性的约束的二次规划来求解，并提供了相应的算法步骤，但是这种方法需要较长的运算时间。Efron(2004)提出用LARS(Least Angle Regression)来求线性模型中LASSO解的轨迹，该方法通过用迭代计算实现求解过程。

Tibshirani(1996)不仅给出了基于线性回归模型的变量选择Lasso惩罚模型，他还将该方法拓展到广义线性模型和比例风险模型中。同时本文还提到了运用LASSO思想处理模型的两个应用，树模型(Tree-based Model)和MARS(Multivariate Adaptive Regression Splines)。

Tibshirani(1996)还做了四个模拟实验，结果表明：

• 对于只包含少数几个非常重要变量的数据集来说，子集选择法表现最好，LASSO表现一般，岭回归法表现最差。
• 对于包含中等数量具有中等重要性解释变量的数据集来说，LASSO表现地最好，岭回归法次之，而子集选择法表现最差。
• 对于包含大量重要性很弱的解释变量的数据集来说，岭回归法表现地最好，LASSO次之，而子集选择法表现最差。

---

• ← Previous Post
• Next Post →